Analysis of a lap around Brands Hatch Indy (Pt. II)
This entry owes very much to a challenge from the Spanish motorsport blog DeltaGap. There, Daniel provides us with a set of real data in order to determine in which sectors the delta time is greater. I took up the challenge and worked out a solution which will help to understand where in a circuit a driver can improve. Is it in the slow corners or in the fast straights?
Contents
The dataset
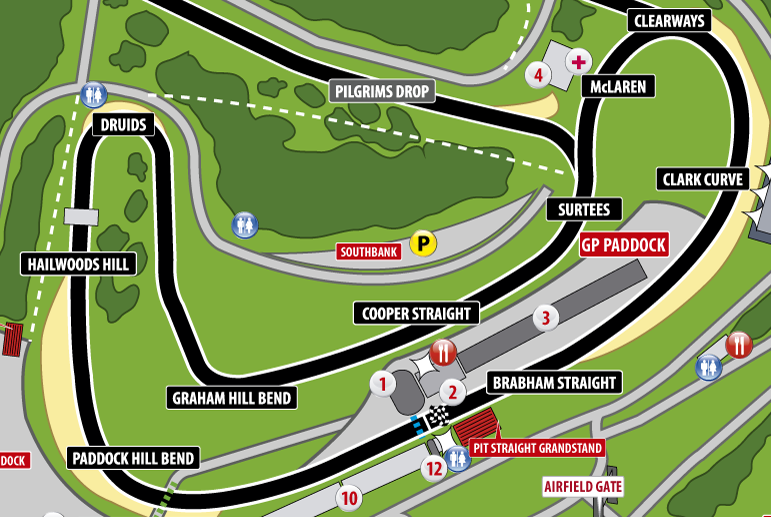
Brands Hatch Indy [1].
The fastest lap of the session was lap #39 (0:42.799), while lap #14 (0:42.864) was the second-fastest one.
The equations
As I’ve seen lately, most people will relate speed and time through the area below the curve. But once we look at the equations, we will realise that this is not the case. By definition, velocity is the rate of change of position with respect to time,
$$ v = \frac{dx}{dt} $$
and thus, the time can be obtained by
$$ dt = \frac{dx}{v} $$
If we were to compute the area under the curve using Riemann sums, i.e., $\sum v\, dx$, we would not get time. That is, time is not related to the area underneath the curve.
Delta time
We can compute the time it takes to travel certain distance as
$$ t = \int\limits_{x_s}^{x_f} \frac{dx}{v(x)} $$
and the delta time between two laps as
$$ \Delta t = t_1 – t_0 = \int\limits_{x_s}^{x_f} \frac{dx}{v_1(x)} – \int\limits_{x_s}^{x_f} \frac{dx}{v_0(x)} $$
where $t_0$ is the reference lap time.
This equation can be simplified, and then
$$ \Delta t = \int\limits_{x_s}^{x_f} \frac{v_0(x) – v_1(x)}{v_1(x) \cdot v_0(x)} \, dx $$
What does this mean? In the numerator we’ve got speed difference, and in the denominator, something very close to speed squared. That is, for a given delta speed —let’s say 1 kph—, the slower the sector of the circuit —the denominator decreases—, the bigger the delta time gets. I’d give up 1 kph in the straights in order to get 1 kph in the corners. Of course that will depend on the circuit. For instance, Monza is a very fast circuit with long high speed sectors while Monaco is a slow one with lots of bends, thus requiring improvements on different areas.
Straights are for fast cars, turns are for fast drivers —Colin McRae.
As Colin McRae said, if you want to improve your car’s laptimes, work the turns with the driver, or just give him a faster car.
Solution
I am using Python —a free and open-source general-purpose, high-level programming language— to solve the equations. More precisely, SciPy, an open-source library for mathematics, science, and engineering.
from scipy.integrate import trapz, cumtrapz
The trapz function will give us the result of computing the integral using the trapezoidal rule.
trapz((v.39 - v.14)/(v.14 * v.39), x=v.index.values)
As the trapezoidal rule is subject to errors, the result will not be 100% accurate, though the closer spaced the points are the smaller the error. In fact, the computed delta time is 0.079 s while the actual delta time at the end of the lap was of 0.065 s.
On the other hand, the cumtrapz function will give us the cumulative values of computing the integral. That is, we will get an array of cumulated delta time values that will give us the delta time in any part of the circuit from the starting line onwards.
Again, errors are cumulative, pretty much like in dead reckoning navigation. Nonetheless, those errors are very small and can be considered acceptable, specially when we are looking for the sectors with greater improvement potential. Those sectors sectors can be spotted as the ones with a steeper delta time curve. Oddly enough, the greatest variations in delta time are found around the slowest corners, just as we asserted earlier.
Acknowledgements
Special thanks to Steve Barker for providing me with vast amounts of data, part of which I used for this blog entry. I would like to take the opportunity to thank Sean Pivek who also provided valuable amounts of data and Craig Scarborough who contributed with a retweet. Many thanks.
References
[1] Brandshatch.co.uk, (2014). Brands Hatch – Circuit Information. [online] Available at: http://www.brandshatch.co.uk/circuit-information.aspx#circuitMap [Accessed 30 Oct. 2014].
