Static pressure, an example with VEGA

On a previous post about static pressure I talked a little bit about its importance in determining altitude. As it seems to me that it was quite an scarce share, I though I should share some results I got from a CFD analysis I did for a class project in collaboration with other two classmates. The object of study was the VEGA expendable launch system.

Figure 1. Vega VV02 ready for liftoff [ESA].

High subsonic, transonic, and supersonic flow regimes were analyzed using the ANSYS FLUENT simulation software. Some of the results were discussed in a report, but here I just want to show the pressure coefficient,

\displaystyle C_p = \frac{p - p_\infty}{q_\infty}

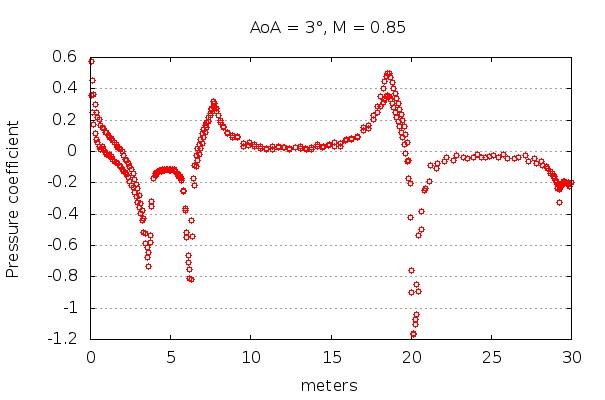
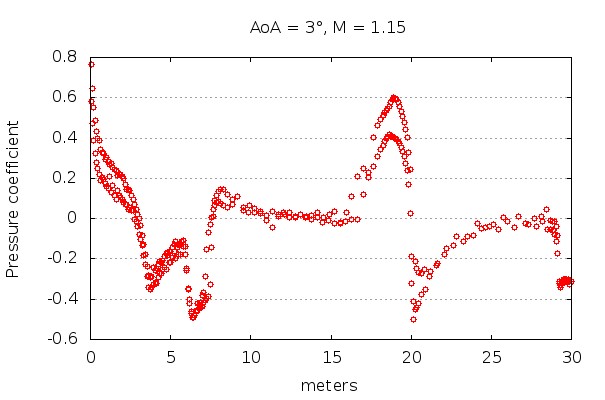
along the lee and the wind side of the rocket at an angle of incidence of 3 degrees.

Figure 2. Pressure coefficient along lee and back side of VEGA, being 0 the tip of the nose cone.

Figure 2. Pressure coefficient along lee and wind side of VEGA, being 0 the tip of the nose cone.

Figure 3. Pressure coefficient at 1.15 Mach along lee and wind side of VEGA.

Figure 3. Pressure coefficient at 1.15 Mach along lee and wind side of VEGA.

As we can see in Figures 2 and 3, there is a region where the static pressure along the surface of the rocket is very close to p∞, which can be used to calculate altitude. This region of static pressure very close to p∞ is located along the second and third stages of VEGA, the narrowest sections of the rocket tube (see Figure 1), and is located at about 3 to 6d downstream from the nose. Those results are consistent with research conducted by Catalano et. al. [1].

Another detail to take into consideration is the fact the region of interest does not change significantly when flying in different flow regimes, thus static pressure taps may yield good results all over different flying conditions when placed correctly.

References

[1] P. Catalano, M. Marini, A. Nicolì, and A. Pizzicaroli. “CFD Contribution to the Aerodynamic Data Set of the Vega Launcher”, Journal of Spacecraft and Rockets, Vol. 44, No. 1 (2007), pp. 42-51.

0
CFD , ,