Physic models in STAR-CCM+ (Part III)
When the Knudsen number
$$ Kn = \frac{M}{Re}\sqrt{\frac{\gamma \pi}{2}} $$
is small, Kn < 0.01, the continuum mechanics formulation of fluid dynamics is valid, and so are the Navier-Stokes equations to which I am allotting Part III of the Physic models in STAR-CCM+ series.
Contents
Fundamental equations
All of fluid dynamics is based on three physical principles:
- Mass is conserved (i.e., mass can be neither created nor destroyed).
- Newton’s second law: F = ma.
- Energy is conserved; it can only change from one form to another.
These physical principles are developed into the fundamental governing equations of fluid dynamics: the continuity, momentum, and energy equations. These equations are also known as transport equations or conservation equations. These equations are also known as transport equations or conservation equations.
Note: all subsequent integrals are closed surface integrals and closed volume integrals.
Continuity equation
Applying the first physical principle to a finite control volume fixed in space, at a point on the control surface, the flow velocity is V and the vector elemental surface area is dS. Also dV is an elemental volume inside the control volume.
$$ \frac{\partial}{\partial t}\iiint\limits_\mathcal{V} \rho\, d\mathcal{V} + \iint\limits_{S} \rho \vect{V} \cdot \vect{dS} = 0 $$
or, alternatively, in in the form of partial differential equation
$$ \frac{\partial\rho}{\partial t} + \nabla\cdot\left( \rho \vect{V} \right) = 0 $$
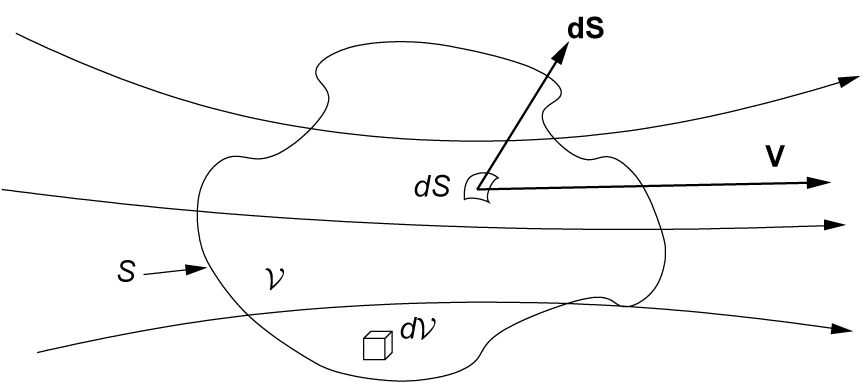
Figure 1. Finite control volume fixed in space.
Momentum equation
Newton’s second law can be rewritten in a more general form as
$$ \vect{F} = \frac{d}{dt} (m\vect{V}) $$
which reduces to F = ma for a body of constant mass. In the equation, mV is the momentum of a body of mass m.
On the left hand side, the force exerted on the fluid as it flows through the control volume comes from two sources:
- Body forces: gravity, electromagnetic forces, or any other forces which “act at a distance” on the fluid inside V.
- Surface forces: pressure and shear stress acting on the control surface S.
On the right hand side, the time rate of change of momentum of the fluid as it sweeps through the fixed control volume is the sum of two terms:
- Net flow of momentum out of control volume across surface S.
- Time rate of change of momentum due to unsteady fluctuations of flow properties inside V.
Hence, Newton’s second law applied to a fluid flow is
$$ – \iint\limits_S p\, \vect{dS} + \iiint\limits_\mathcal{V} \rho \vect{f}\, d\mathcal{V} + \vect{F}_\text{viscous} = \frac{\partial}{\partial t}\iiint\limits_\mathcal{V}\rho\vect{V}\, d\mathcal{V} + \iint\limits_S (\rho\vect{V}\cdot\vect{dS})\vect{V} $$
which can be rewritten as partial differential equations that relate flow-field properties at any point in the flow,
$$ \frac{\partial(\rho u)}{\partial t} + \nabla\cdot (\rho u \vect{V}) = -\frac{\partial p}{\partial x} + \rho f_x + (\mathcal{F}_x)_\text{viscous} \\
\frac{\partial(\rho v)}{\partial t} + \nabla\cdot (\rho v \vect{V}) = -\frac{\partial p}{\partial y} + \rho f_y + (\mathcal{F}_y)_\text{viscous} \\
\frac{\partial(\rho w)}{\partial t} + \nabla\cdot (\rho w \vect{V}) = -\frac{\partial p}{\partial z} + \rho f_z + (\mathcal{F}_z)_\text{viscous} $$
where the subscripts x, y and z on f and F denote the x, y and z components of the body and viscous forces, respectively.
Adopting an infinitesimally small moving fluid element of fixed mass a the model of the flow, and applying Newton’s second law in the form of F = ma we can get to
$$ \rho \frac{Du}{Dt} = – \frac{\partial p}{\partial x} + \frac{\partial\tau_{xx}}{\partial x} + \frac{\partial\tau_{yx}}{\partial y} + \frac{\partial\tau_{zx}}{\partial z} \\
\rho \frac{Dv}{Dt} = – \frac{\partial p}{\partial y} + \frac{\partial\tau_{xy}}{\partial x} + \frac{\partial\tau_{yy}}{\partial y} + \frac{\partial\tau_{zy}}{\partial z} \\
\rho \frac{Dw}{Dt} = – \frac{\partial p}{\partial z} + \frac{\partial\tau_{xz}}{\partial x} + \frac{\partial\tau_{yz}}{\partial y} + \frac{\partial\tau_{zz}}{\partial z} $$
These are the momentum equations in the x, y and z directions, respectively. They are scalar equations and are called the Navier-Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes.
Energy equation
For a study of incompressible flow, the continuity and momentum equations are sufficient tools to do the job. However, for a compressible flow, we need an additional fundamental equation to complete the system. This fundamental relation is the energy equation.
The physical principle on which the energy equation lies is the first law of thermodynamics,
Energy can be neither created nor destroyed; it can only change in form.
which can be stated as
$$ \delta q + \delta w = de$$
where δq and δw represent an incremental amount of heat and work respectively, which are forms of energy, that when added to the system, change the amount of internal energy de in the system. This physical principle, through a control volume, can be directly translated into
$$ \begin{multline}
\iiint\limits_\mathcal{V} \dot{q}\rho\,d\mathcal{V} + \dot{Q}_\text{viscous} – \iint\limits_S p \vect{V}\cdot\vect{dS} + \iiint\limits_\mathcal{V} \rho (\vect{f}\cdot\vect{V})\,d\mathcal{V} + \dot{W}_\text{viscous}\\
= \frac{\partial}{\partial t} \iiint\limits_\mathcal{V}\rho \left( e + \frac{V^2}{2} \right)\,d\mathcal{V} + \iint\limits_S \rho \left( e + \frac{V^2}{2} \right)\vect{V}\cdot\vect{dS}
\end{multline}$$
and in the form of partial differential equations as
$$ \begin{multline}
\frac{\partial}{\partial t} \left[ \rho \left( e + \frac{V^2}{2} \right) \right] + \nabla\cdot \left[ \rho \left( e + \frac{V^2}{2} \right) \vect{V} \right] \\
= \rho\dot{q} – \nabla\cdot (p\vect{V}) + \rho(\vect{f}\cdot\vect{V}) + \dot{Q}’_\text{viscous} + \dot{W}’_\text{viscous}
\end{multline} $$
where $\dot{Q}’_\text{viscous}$ and $\dot{W}’_\text{viscous}$ represent the proper forms of the viscous terms.
Summary
These equations are fundamental to all of aerodynamics making a total of 5 equations with five accompanying independent variables, namely pressure, three components of velocity and temperature. Also, a thermodynamic equation of state can be added to the set to relate density to the pressure, temperature, and composition.
Exact analytical solutions of the complete Navier-Stokes equations exist for only a few very specialized cases.
Fortunately, many problems of engineering interest are adequately described by simplified forms —by deleting superfluous terms— of the full conservation equations, which can often be solved easily.
References
[1] User Guide STAR-CCM+ Version 8.06. 2013.
[2] Anderson, J. 2007. Fundamentals of aerodynamics. 4th ed. Boston: McGraw-Hill Higher Education.
[3] Ganić, E., Hicks, T. and Predko, M. 2003. McGraw-Hill’s Engineering Companion. New York: McGraw-Hill.
