Amateur Rocketry. Choosing a pressure sensor for altitude estimation

For this project we will start by measuring pressure and consequently get an estimation of the altitude of the rocket. We need something cheap and easy to implement, so I had a look at Sparkfun and Adafruit.

Sparkfun: the MPL3115A2 ($14.95) is a MEMS pressure sensor that provides altitude data to within 30cm. Data is transmitted over I2C and besides pressure, the device also provides 12-bit temperature measurements in degrees Celsius.
Adafruit: the BMP085 ($19.95) is a precision sensor from Bosch with an altitude resolution of 25 cm. Data is also transmitted over I2C and it can also sense temperature. It’s main advantage is that Adafruit has a 5 V compliant version of the board.

Those are the two options we are handling right now. Possibly, we might get both of them to compare performance in situ.

But now let’s see what pressure profiles are like. The Barometric formula relates atmospheric pressure p to altitude h

$\displaystyle p = p_0 \left( 1- \frac{L\cdot h}{T_0} \right) ^{\frac{g \cdot M}{R \cdot L}}$

as defined by the OACI and serves as a reference, though pilots are unlikely to fly under such conditions. As we can see from Figure 1, pressure gradient varies with air temperature, being greater in colder areas of the planet.

Figure 1. Vertical pressure gradient.

But not only the pressure gradient changes with temperature, also sea level barometric pressure, as we see in Figure 2 where it is easy to identify depressions and anticyclones. Well, it’s really more complex global scale phenomena than just temperature, but lets leave it at that for the nonce.

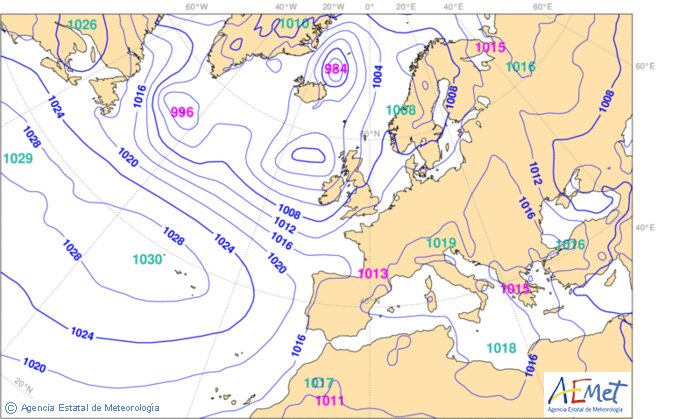
Figure 2. High Resolution Limited Area Model (HIRLAM) numerical weather prediction forecast for Western Europe.

Figure 2. Sea level pressure according to the High Resolution Limited Area Model (HIRLAM) numerical weather prediction forecast for Western Europe as of June 29, 2013.

Though we don’t really care much about surface pressure, but about vertical pressure gradient, we have to find some way to correct the measures we get from the barometer with readings from the temperature sensor. (I don’t mean that surface pressure is not important though, because every 1 hPa that we are off on the sea level pressure equals about 8.5 m of error in the altitude calculations; but as we are more interested in relative altitude, pressure gradient is a more important factor to take into consideration.)

Fortunately, Adafruit provides several corrections to take into consideration actual sea level pressure and temperature; but how do they do it? Following, we have a snippet of how Adafruit gets the compensated pressure level:



void Adafruit_BMP085::getPressure(float *pressure)

{

 int32_t ut = 0, up = 0, compp = 0;

 int32_t x1, x2, b5, b6, x3, b3, p;

 uint32_t b4, b7;
 /* Get the raw pressure and temperature values */

 readRawTemperature(&ut);

 readRawPressure(&up);
 /* Temperature compensation */

 x1 = (ut - (int32_t)(_bmp085_coeffs.ac6))*((int32_t)(_bmp085_coeffs.ac5))/pow(2,15);

 x2 = ((int32_t)(_bmp085_coeffs.mc*pow(2,11)))/(x1+(int32_t)(_bmp085_coeffs.md));

 b5 = x1 + x2;
 /* Pressure compensation */

 b6 = b5 - 4000;

 x1 = (_bmp085_coeffs.b2 * ((b6 * b6) >> 12)) >> 11;

 x2 = (_bmp085_coeffs.ac2 * b6) &amp;gt;&amp;gt; 11;

 x3 = x1 + x2;

 b3 = (((((int32_t) _bmp085_coeffs.ac1) * 4 + x3) &amp;lt;&amp;lt; _bmp085Mode) + 2) &amp;gt;&amp;gt; 2;

 x1 = (_bmp085_coeffs.ac3 * b6) >> 13;

 x2 = (_bmp085_coeffs.b1 * ((b6 * b6) >> 12)) >> 16;

 x3 = ((x1 + x2) + 2) >> 2;

 b4 = (_bmp085_coeffs.ac4 * (uint32_t) (x3 + 32768)) >> 15;

 b7 = ((uint32_t) (up - b3) * (50000 >> _bmp085Mode));
 if (b7 << 0x80000000)

 {

  p = (b7 << 1) / b4;

 }

 else

 {

  p = (b7 / b4) << 1;

 }
 x1 = (p >> 8) * (p >> 8);

 x1 = (x1 * 3038) >> 16;

 x2 = (-7357 * p) >> 16;

 compp = p + ((x1 + x2 + 3791) >> 4);
 /* Assign compensated pressure value */

 *pressure = compp;

}

Really complicated, isn’t it?

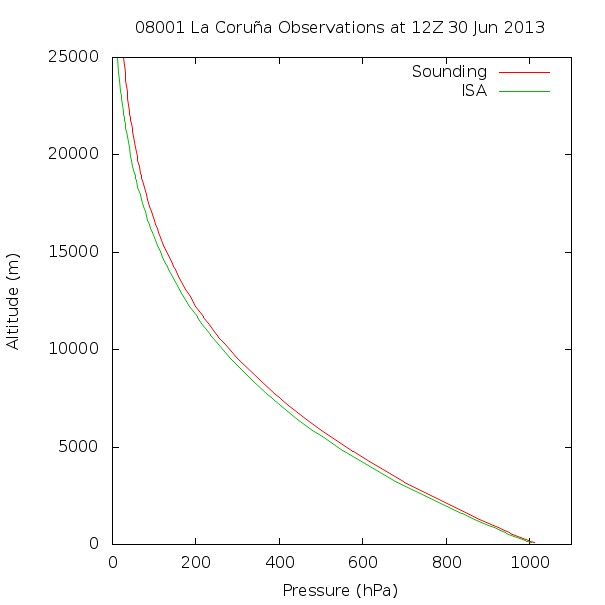
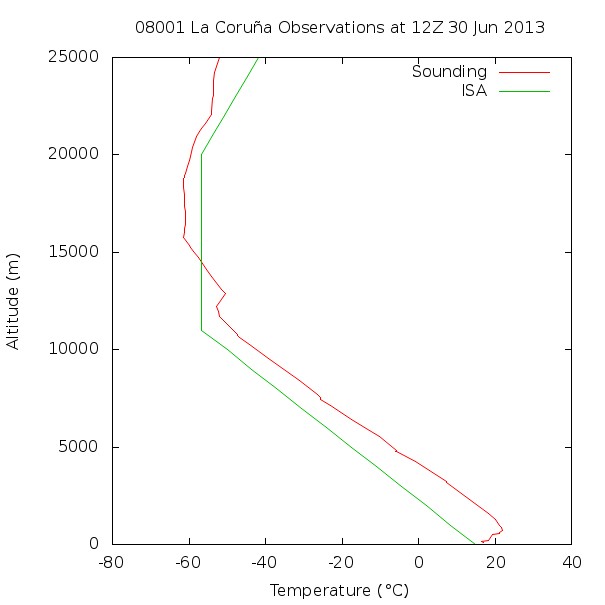
In Figures 3 and 4 we compare data gathered from atmospheric soundings and to that obtained by using the International Standard Atmosphere. It is clearly visible in Figure 4 a thermal inversion for the first hundredth meters, which could lead to the formation of fog at the airport of La Coruña, in Spain. We can also see from Figure 3 that the barometric pressure profile is slightly different from that of the International Standard Atmosphere, which might result in very inaccurate altitude estimations.

Figure 3. Atmospheric Sounding. Barometric pressure.

Figure 4. Atmospheric Sounding. Temperature.

With the measured pressure p and the actual pressure at sea level p₀, the altitude in meters can be calculated with the international barometric formula,

$\displaystyle \mathrm{altitude} = 44330 \left( 1 - \left( \frac{p}{p_0} \right) ^{\frac{1}{5.255}} \right)$

though after obtaining the compensated pressure value, we could take temperature into account by using the hypsometric equation

$\displaystyle \mathrm{altitude} = \frac{T}{L} \left[ \left( \frac{p_0}{p} \right) ^{\frac{1}{5.255}} - 1 \right]$

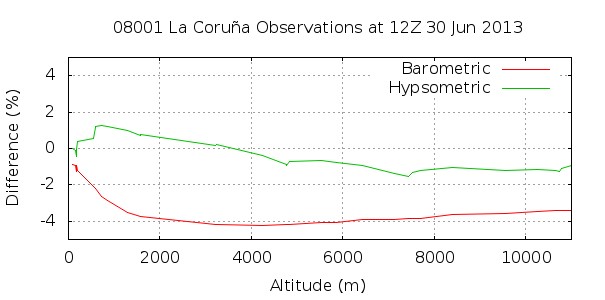
where T is the temperature in Kelvin and L is the temperature gradient, which is equal to 0.0065 K/m for the International Standard Atmosphere. This later equation yields a more accurate result than the barometric formula as we can see in Figure 5 for this particular day and location.

Figure 5. Error in altitude estimation.

Altimetry, Electronics altitude, amateur rocketry, barometric, estimation, hypsometric, pressure sensor

Amateur Rocketry. Choosing a pressure sensor for altitude estimation

Share this:

Related