James Bond’s Wet Nellie
Few fictional characters are as famous as Ian Fleming’s James Bond. Proof of that is James Bond ‘s film franchise is one of the highest-grossing media franchises of all time.
The Bond films are renowned for a number of features, among which subtly modified cars, guns, and gadgets supplied by Q Branch stand out. It is precisely of one of those cars designed by Q that this article is about.
The iconic Aston Martin DB5 will surely come to mind as the most outstanding car of the entire saga. It is indisputably gorgeous and not without equipment; it includes an ejection system, twin machine guns, tire slasher, bullet-proof screen, oil slick sprayer and a long etcetera.

But let’s leave aside the DB5 and focus on the second most famous car of the British Secret Service agent.
Contents
The Lotus Esprit S1 Wet Nellie
Not as famous as the 1964 DB5, but certainly the most impressive transformer car in the series. Also developed by Q Branch, the Lotus Esprit S1 was given amphibious capabilities as well as weaponry and safety equipment. During amphibious mode, the wheel arches turn into fins, and a small periscope on the roof enables 007 to navigate at speed underwater.

The Lotus Esprit S1 featured in The Spy Who Loved Me (1977) and was referred to as Wet Nellie, in reference to Little Nellie, an autogyro featured in You Only Live Twice (1967).
CAD model
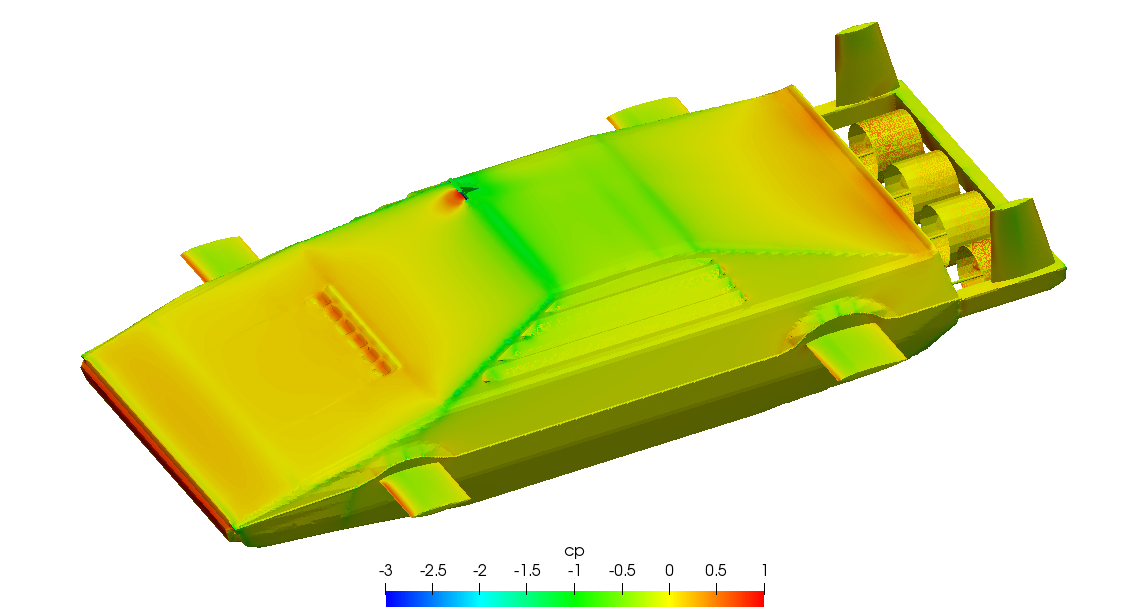
A simplified Wet Nellie CAD model is freely available from the SketchUp 3D Warehouse in a couple of formats that can be easily converted to STL using online tools. I then just removed the rocket launchers and windshield grilles, grilles which I didn’t see featured in the film the way they were represented in the model. The result is what we have in the following figure.

Simulation model
The whole setup is carried out in SimScale —have a look at the public project— and is my entry to the SimScale Community Contest 2019.
Mesh
The backend mesher used by the platform is snappyHexMesh; which requires a background mesh, that in this case is of size 50 × 20 × 10 m3 composed of cubes of 0.5 m side. For this model, the smallest cells size is 2 mm in the propeller region and 4 mm for the rest of the vehicle. Refinement regions around the propellers and the wake of the submarine have been defined.

The propellers are enclosed in a cell zone so that a rotating condition —through the MRF model— can be imposed.
Initial and boundary conditions
The fluid is defined as saline water (3.5 %) with a density ρ of 1024.065 kg/m3 and a kinematic viscosity ν of 9.88e-7 m2/s. A very different environment to what I’m used to [air]. The boundary conditions used for this problem are detailed below —the initial conditions for the internal field are based on the values defined for the inlet.
| Boundary: | inlet | outlet | farfield | submarine |
| p | zeroGradient | fixedValue uniform 0 | zeroGradient | zeroGradient |
| U | fixedValue uniform (2.5 0 0) | zeroGradient | slip | fixedValue uniform (0 0 0) |
| k | fixedValue uniform 0.00023 | zeroGradient | zeroGradient | kqRWallFunction uniform 0 |
| omega | fixedValue uniform 237 | zeroGradient | zeroGradient | omegaWallFunction uniform 0 |
| nut | calculated uniform 0 | calculated uniform 0 | calculated uniform 0 | nutkWallFunction uniform 0 |
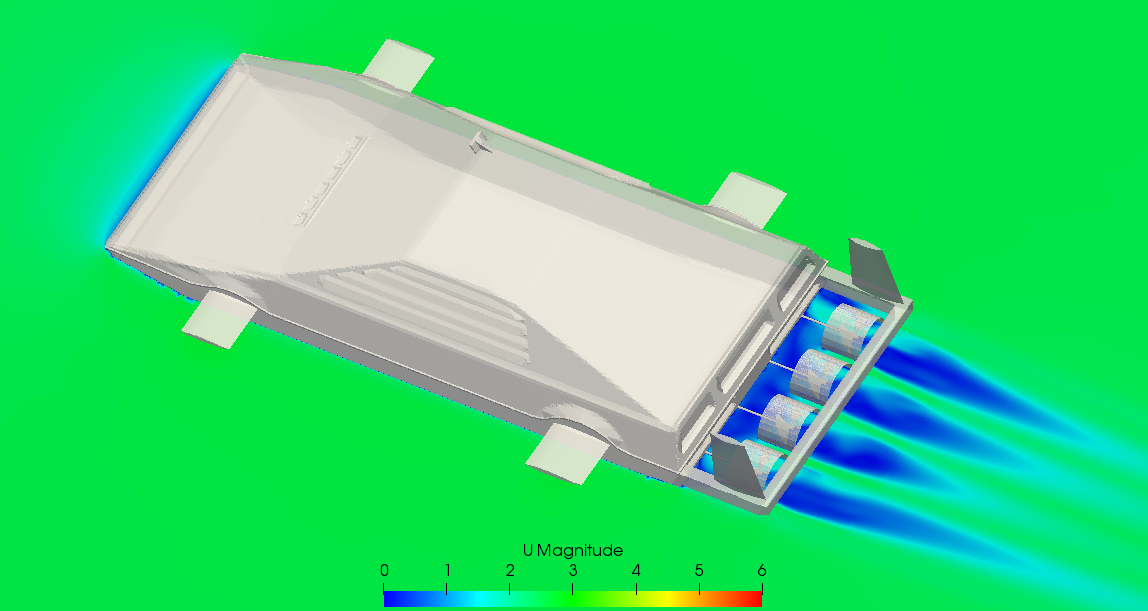
A speed of 2.5 m/s is defined which is based on the speed Wet Nellie has in the film, measured as the time it takes for the submarine to pass next to an immobile coral bottom. The rotational speed of the propellers was also obtained through the film scenes. Each blade takes about 22 frames to turn 360°, and since the film is played back at 25 fps, this gives us a turning rate of approximately 5.5 radians per second.

As we will see later, though, the 5.5 rad/s is quite a slow speed for our model. So, ran an additional simulation imposing a rotational speed of 100 rad/s (~950 rpm) for comparison.
Simulation results
Very interesting things could be analysed on the basis of this model, but for now I will focus only on drag and the effect of the propellers on it.
Drag
Let’s see how they [propellers] alter the drag in the following graph.