DrivAer: fastback vs estate back aerodynamics
I own myself a fastback Mazda 6, but also like estate back versions of certain models like the BMW 3-series. So, I’m curious about the aerodynamic performance delivered by both body styles. Luckily enough, the Technical University of Munich has developed a realistic car model intended to replace the Ahmed body used in investigations in automotive aerodynamics. The DrivAer model was introduced circa 2011 and features three body styles: fastback, estate back, and notchback. This styles can be combined with different wheels, underbodies, and engine bay allowing for 18 distinct configurations. The CAD data of the DrivAer model is available on request.
There is also plenty of research carried around those geometries, so that it is possible to validate our simulations.
Contents
Computational domain
Although the Master’s thesis by Yazdani (2014) is quite comprehensive, his smallest volume discretization consisted of circa 50 million-cells; well above my personal computational resources, even though I were to consider symmetry. For this reason, I took some hints from the work by Shinde et al. (2013) in order to get a representative enough computational domain with a fraction of the cell-count while keeping drag estimations within 5 % of experimental results.
Mesh
The model simulates a 1:2.5 scaled down DrivAer vehicle inside a virtual wind tunnel of size 28 × 10 × 7 m³. This results in a blockage ratio of 0.57 %. For a symmetry case, we get 9.1 million cells, with 5 boundary layer cells around targeting a y+ of 30.
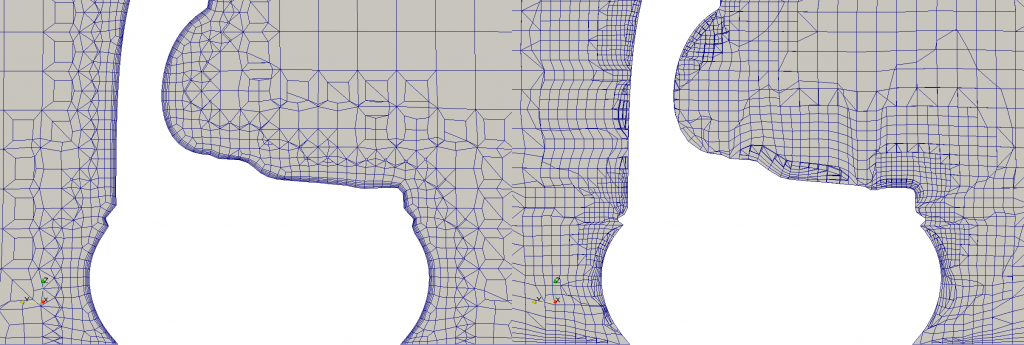
The mesh was generated with cfMesh. As I was struggling to get a good boundary layer coverage of the DrivAer model using snappyHexMesh —which in turn impaired simulation results—, I turned to this other mesher that claimed to achieve 100 % boundary layer coverage with minimal settings. And I have to admit that I was pleasantly surprised by the results.
In the image above we can see side by side the results I achieved using both meshers: cfMesh on the left, and snappyHexMesh on the right. The boundary layer coverage I got with snappyHexMesh is chaotic at best —and I tried many different settings and spent a great deal of time at CFD Online looking for settings to improve mesh quality—. With cfMesh, on the contrary, with just a few settings I got a really neat mesh, and in one third of the time.
The only important thing I am not considering for this simulation is MRF; as I don’t know yet how to properly mesh a separate cell zone with cfMesh.
Boundary and initial conditions
Following the settings portrayed by Shinde et al. (2013), the inlet velocity is set to 40 m/s, with turbulent initial conditions estimated following best practice guidelines —turbulent kinetic energy k of 0.0096 m²/s² and specific turbulent dissipation rate ω of 61.935 s–¹. The following table defines al the boundaries specified at time 0:
| Boundary | p | U | k | omega | nut |
| inlet | zeroGradient | fixedValue uniform (40 0 0) | fixedValue uniform 0.0096 | fixedValue uniform 61.935 | calculated uniform 0 |
| outlet | fixedValue uniform 0 | zeroGradient | zeroGradient | zeroGradient | zeroGradient |
| tunnel | zeroGradient | slip | kqRWallFunction uniform 0.0096 | omegaWallFunction uniform 61.935 | nutUSpaldingWallFunction |
| floor | zeroGradient | movingWallVelocity uniform (40 0 0) | kqRWallFunction uniform 0.0096 | omegaWallFunction uniform 61.935 | nutUSpaldingWallFunction |
| car | zeroGradient | movingWallVelocity uniform (0 0 0) | kqRWallFunction uniform 0.0096 | omegaWallFunction uniform 61.935 | nutUSpaldingWallFunction |
| symmetry | symmetryPlane | symmetryPlane | symmetryPlane | symmetryPlane | symmetryPlane |
Results
The total drag value for the two models corresponds to a configuration with smooth underbody and no rotating wheels. The following table shows the average simulated drag value and the corresponding experimental one from Mack et al (2012) for smooth underbody and stationary ground configuration (GS off).
| Model | Expt. Cd | CFD Cd | Error | |
| Fastback | 0.249 | 0.248 | -0.40 % | -1 ct |
| Estate back | 0.286 | 0.273 | -4.55 % | -13 ct |
Correlation is quite good. Just as is the case with Shinde et al. (2013) and Yazdani (2015), we get better correlation with the fastback model.
The previous plot shows the accumulated drag for both fastback and estate back. We can see the influence of the difference in the geometry of the back as far forward as in the front axis. But in this post I am only going to focus my attention on the rear end where the differences are most noticeable.
Pressure
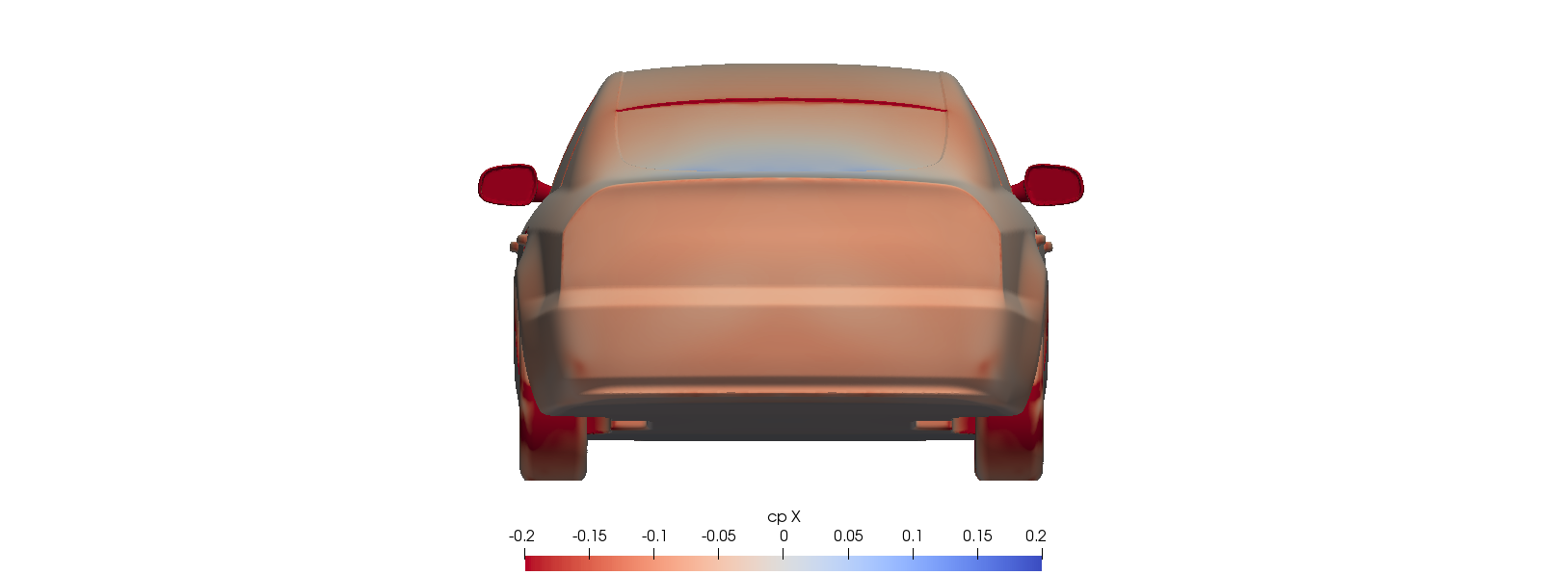
The most elemental visualisation used to spot drag inducing areas is that of pressure contours —out of the two components of drag, pressure and shear stress, the former plays the leading role—. In the following slideshow we show images of the x-component of the pressure coefficient for both fastback and estateback models.
As expected, the estateback offers pressure a larger close to vertical surface area to pull from. On the other hand, the lower part of the rear window in the fastback model, where the trunk straightens up, contributes a small increase in pressure that slightly reduces drag —evidenced by the light blue colour.
The following images show total pressure —an indicator of the useful energy density contained within the flow—. Part of this energy is dissipated in the wake through turbulence in what’s called the energy cascade.
The rear end of the fastback model sends “fresh” air downwards and thus the wake is smaller. We’ll go into more detail on that in the following section.
Velocity
As mentioned previously, the wake of the fastback model is smaller due to the downwash favoured by the gentle curvature of the roof and rear window. This is shown in the line integral convolution images of the symmetry plane.
Although real flow is unsteady, steady state RANS simulations allows us to identify the macrostructures in which separation bubbles contain circulation, and the axes of those vortices. This is precisely one of the aspects of fluid motion we can identify using LIC images. It is readily apparent that the fastback model has two such bubbles in the rear, while the estate back only develops one bubble close to the lower part of the rear fender —also seen in the studies conducted by Yazdani (2015).
There’s another way to identify macrostructures, and that’s using some of the Galilean invariant vortex detection algorithms available in OpenFOAM. In this case, I have used the Lambda2 method.
We can see several of those structures using isosurfaces with constant Lambda2. As a reference, I’m also showing some schematics drawn by Hucho and Ahmed (1987) so that we can better identify the basic structures. As mentioned earlier, structures A and B are present in the fastback model as well as structure C, though less intense due to a smother c-pillar. The estate back model only has vortical structures A and C.
References
Heft, A. I., Indinger, T., & Adams, N. A. (2012). Experimental and Numerical Investigation of the DrivAer Model (pp. 41-51). ASME.
Hucho, W.-H., & Ahmed, S. R. (1987). Aerodynamics of road vehicles: from fluid mechanics to vehicle engineering. London: Butterworths.
Mack, S., Indinger, T., Adams, N. A., Blume, S., & Unterlechner, P. (2012). The Interior Design of a 40% Scaled DrivAer Body and First Experimental Results (p. 75). ASME.
Shinde, G., Joshi, A., & Nikam, K. (2013). Numerical Investigations of the DrivAer Car Model using Opensource CFD Solver OpenFOAM.
Yazdani, R. (2015). Steady and Unsteady Numerical Analysis of the DrivAer Model (MSc Thesis). Chalmers University of Technology, Göteborg.